Contents
- Index
Limits in MODELS
Limits on expressions are generally specified {min:a max:b}
Limits are generally used to restrict variables inside certain ranges.
The first example illustrates constraints on derivatives.
MODEL derivlim
CONST freq {val: 50}
omega {val: 2*pi*freq}
half_period {val: 0.5/freq}
VAR x -- applied signal
dx -- derivative of x
dxlim -- derivative of x with limits
y -- integral of dxlim
INIT
histdef(x) :=0; -- needed for calculation of deriv()
histdef(dxlim) :=0; -- needed for calculation of integral()
histdef(integral(dxlim)) :=0; -- needed for calculation of integral()
ENDINIT
EXEC
x:= (1 -cos(omega*t))*(t<=3*half_period) -- active until t=half_period
+ 2*(t>3*half_period) -- active after t=half_period
dx:= deriv(x)
dxlim := dx {max: 0.6*omega} -- limits the derivative
y:= integral(dxlim) -- reconstructs signal with limit applied on derivative
ENDEXEC
ENDMODEL
The next example illustrates dynamic limit on integral in MODELS.
Only dynamic limits are allowed directly on integral {dmin:a dmax:b}
A static limits can be set on the integral value after evaluation of the integral.
MODEL ilim
VAR x, y -- step signal =1 from t=0 to t<=1, =-1 for t>1
dlim -- integral(x), dynamic limit=0.7
nolim -- integral(y), no limit
slim -- static limit=0.7 applied to 'nolim'
HISTORY x {dflt: 0}
y {dflt: 0}
integral(x) {dflt: 0}
integral(y) {dflt: 0}
EXEC
x:= 1
IF t>1 THEN
x:= -1
ENDIF
y:= x
dlim :=integral(x){dmax: 0.7}
nolim :=integral(y)
slim :=nolim {:0.7}
ENDEXEC
ENDMODEL
A dynamic limit means that the derivative of the output is set to zero when the unrestricted output is outside the limits. For integrals this means that the integrand is set to zero as long as its contribution causes the output to break the limits. In the example above the integrand in integral(x) x is set to zero when dlim is larger than 0.7 and x>0 (positive contribution to the integral).
A static limit is the most normal case and applies directly on the unlimited variable.
Fig. 1 shows the result of ilim model above. x is drawn as a thick line and nolim, slim and dlim indicated as Nolimit, static limit and dynamic limit respectively.
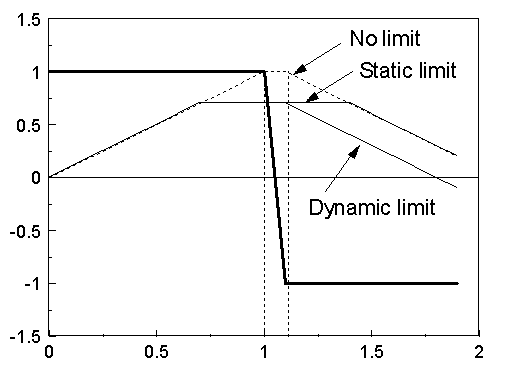
Fig. 1. Results of the model ilim.
