ATPDraw calls a procedure BuildC that creates the C-matrix. This matrix is split in two halves and connected to each terminal of the transformer. The type 1, 2 … PI-equivalent is used with the series resistance set to infinity (1e8 W) to accomplish this.
The capacitance matrix C is based on the following two matrices
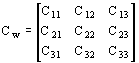 and
and 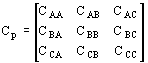
The Cw matrix contains the capacitances between windings1-3 that are equal for all phases.
The Cp matrix contains capacitances that are specific to phase A, B, or C. These are typically connected to the outer windings.
The total C-matrix is then built on these two matrices dependent on the type of winding (pancake/cylindrical). After adding these matrices the total C-matrix is sorted according to A1, A2, A3, B1, B2, B3, C1, C2, C3 where ABC is the phase number and 123 is the winding number.
Pancake:
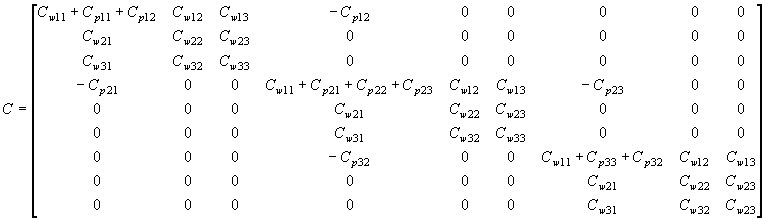
Cylindrical:

The C-matrix is then sorted in the sequence PST winding sequence based on the user's choice of winding number.
Typical values
A capacitive coupling factor Kc can be specified by the user with a default value of 0.3.
The MTU reports use the concept of transient recovery voltage (TRV) to obtain the effective capacitance when the inductance is known. The IEEE standard C37, fig. B2 is used to obtain the frequency of the TRV for a known voltage level and fault current. In order to use these curves in ATPDraw a fitting function had to be established. The function is on the form
![]() [mF]
[mF]
with U in [kV], S in [MVA] and ![]() [kA]
[kA]
The essential fitting function is approximated by
![]() [kHz]
[kHz]
 Fig. 1. Result of the fitting function above. To be compared to IEEE C37, fig. B2.
Fig. 1. Result of the fitting function above. To be compared to IEEE C37, fig. B2.
In the case of an auto-transformer the Xpu values are scaled as explained under the reactance part.
In the case of typical values the Cp matrix (between phases) is always set to zero in lack of any better choice.
For a two-winding transformer the Cw matrix is calculated as
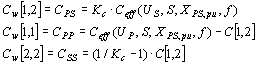
For a three winding transformer the typical capacitance more complicated. Here a simple approach is used and the two other coupling factors used in MTU6, p. 34 are avoided. Instead the following relations are used:

This approach could be further discussed.
Test report
In the test report the capacitances between each winding and ground and between all windings is assumed to be directly specified while the Cp matrix is set to zero. All values must be specified per phase. An option for specifying Cp is built into the code, but this is hidden at the moment due to lack of a test case.
Design data
The calculation of design data capacitances are based on MTU7 chapt. 5.3, p. 33-42. The user has to specify the winding geometry as well as the various equivalent permittivities of insulation system. The same configuration as given in fig. 4 is used here.
Cylindrical windings:
Capacitance between two windings:
 (C.1)
(C.1)
The subscript syntax is H=outer, L=inner (the capacitance between the inner and outer in a three-winding situation is assumed to be zero). Where h is the average height of the two windings involved and Dh is the width of the leakage channel between them (added to compensate for end effects). dH,i is the inner diameter of the outer winding, while dL,o is the outer diameter of the inner winding. The capacitance between the inner winding and the core is approximated the same way, but with Dh set to the width of the inner leakage channel (the capacitance between the other windings and the core is ignored).
Capacitance between the outer windings of adjacent legs:
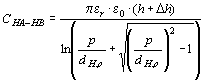 (C.2)
(C.2)
Where p is the phase distance and dH,o is the outer diameter of the outer winding. In this case the end effect factor becomes Dh = p- dH,o.
The remaining capacitances considered are the one between the outer winding and the tank. The capacitance between the end phase (outer winding) and the tank is calculated from (C.1) replacing dH,i and dL,o by dH,o and t, respectively, where t is the tank diameter. The capacitance is further multiplied by a factor 0.75 to account for a non-circular tank. The capacitance between the middle phase (outer winding) and the tank is calculated from (C.2) replacing p by t, setting Dh to the distance between the outer winding surface and the tank wall Dh =(t- dH,o)/2. In this case the capacitance is multiplied by a factor 0.25.
Pancake windings:
Capacitances between all windings and the core are calculated by (C.1) replacing h by the winding width b, and Dh by the width of the inner leakage channel, a1.
The capacitance between two windings is calculated by a parallel plate approach:
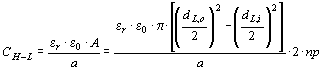 (C.3)
(C.3)
Where a is the height of the leakage channel between the windings, and np is the number of pancakes. dL,i is the inner diameter of the L-winding (c+2\\a1 in fig. 4).
The capacitance between the adjacent phases is assumed to be between windings 1 (L=inner) and this can be calculated by (C.3) replacing a by the distance between the outer parts of the windings.
Capacitances between windings and the tank are approximated by (C.1) replacing h+Dh by the total winding width b. (the number of pancakes is included in b). Further dH,i is replaced by the tank width t, and finally a reduction factor 0.25 is applied. In addition the winding 1 (L=inner) of the outer phases will have a capacitance to the end tank wall. This can be approximated by (C.3) replacing a by the distance to the tank wall q, and by setting 2\\np to unity.
The capacitance matrix Cw is built up like a nodal admittance matrix consisting of those capacitances that are equal for all phases. The capacitance matrix Cp consists of the quantities that are unique for each phase. Thus Cp contains the capacitances between the outer windings on adjacent legs and between these windings and the tank. The concept 'outer winding' will be different for pancake and cylindrical windings.