ATPDraw obtains the winding resistances by calling a routine BuiltR. The winding resistances are written to the ATP-file from nodes PST with extension ABC/DEF to nodes PST with extension XYZ. If the user selects a frequency dependent winding resistance the resistance is approximated by a two-cell Foster equivalent. A negative compensating (to minimize the imaginary part) inductance Leq is connected between node PST with extension 'UVW' and PST with extension 'XYZ'. This inductance can in some cases result in an unstable solution and this needs to be further investigated.
Typical values
The typical winding resistances (at power frequency) are in principle based in the MTU7 table 5 at page 53 (from A. Greenwood: Electrical Transients in Power Systems, Wiley 1991). However, since the kV and kVA values tabulated are rather limited (up to 50 MVA and 230 kV) a simple interpolation approach as used for the reactance can not be utilized here. Instead a function Rw is established that takes in the parameter u [kV] and s [MVA] and returns the resistance in %. Data for a 290 MVA/ 430 kV transformer was used along with table 5 to calibrate the function:
![]() [%]
[%]
Test report
The test report data are given at power frequency only, and the DC resistance utilized in MTU7 eq. (32) p. 46 is not used in ATPDraw. The per unit short circuit resistances are calculated from the test report data (positive sequence)
RPS=PPS/[kW]/(1000*SPS[MVA]) [pu]
RST=PST/[kW]/(1000*SST[MVA]) [pu]
RPT=PPT/[kW]/(1000*SPT[MVA]) [pu]
And the winding resistance is assumed to be equally shared between the windings in the case of a two-winding transformer (RP=RPS/2 and RS= RPS/2. In the case of a 3-winding transformer the traditional star-equivalent approach is used:
RP=(RPS+RPT-RST)/2 [pu]
RS=(RPS+RST-RPT)/2 [pu]
RT=(RPT+RST-RPS)/2 [pu]
In the case of an auto-transformer the short circuit resistances are scaled similarly as the reactance
RST =1/(UP-US)*(RST*UP*US/(UP-US)+RPS*UP-RPT*US);
RPS =RPS*sqr(UP/(UP-US));
Design data
The user can specify the winding conductivity s, the equivalent cross section of each turn A, the average length of each turn L, number of turns of the inner winding, and the rated voltages of all windings. The DC resistance is then simply calculated as in eq. (36) p. 51 of MTU7 and scaled to the power frequency using the frequency dependency below (with nl=1). The user has to specify the conductor height and width and the number of conductors in parallel. In the resistance is assumed to be frequency independent only the total area matters (product of width, height and #parallel).
![]()
where N is the number of turns, L is the average length per turn, wt and ht is the width and height of each conductor respectively, and np is the number of parallel conductors.
Frequency dependency
The frequency dependent resistance is calculated at 11 logarithmically space frequency points from 0.1 to 10 kHz. The frequency dependent resistance is then fitted by a two-cell (R||L) Foster equivalent circuit. The inductive part of the Foster equivalent is partly cancelled by a negative additional inductance. The fitting of the winding resistance can be studied by clicking the View R(f) button.
The resistance variations can from ATPDraw v5.8 be based on two different approaches; In the first approach the resistance is assumed to follow
![]()
where R0 is the resistance at the power frequency f0. The second approach is for typical and test report source of data assumed to follow the X/R ratios for a 100 MVA transformer from for Cigre WG 13-05, Electra p. 17-42, 1975, assuming a constant inductance. For design data the resistances are assumed to follow (eq. (37) is MTU7):
![]()
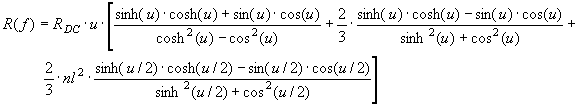
Here wt is the width of a single conductor. Further nl is the number of layers in the winding.
The inductance can also follow two different models; The first is a constant value (as given be the power frequency leakage inductance) and the second is a variation according to a Kramers-Kronig relation (based on R(f) with a sqrt(f) extrapolation).
The fitting routine based on the quasi-Newton (L-BSGF) optimization method. The routine minimizes the object function OF (a combination of the real and imaginary part of the Forster equivalent impedance) over the 11 frequency points, with Rm and Lm being the measured/estimated values as function of frequency. Three Foster cells might be too little for an accurate fit.
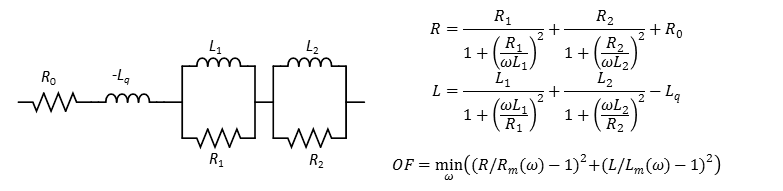
The negative inductance must be less than the corresponding element of the A-matrix in order to get a numerical stable solution. L1+L2<1/a. If this constaint is violated the two inductances are set L1=L2=1/(2*a) and the resistances R1 and R2 are used for the fitting.